COURBES ALGÉBRIQUES

COURBES ALGÉBRIQUES

En fondant la géométrie analytique, Descartes avait substitué au plan de la géométrie d’Euclide l’ensemble R² des couples de nombres réels et, de ce fait, à la notion de courbe, celle d’équation. La construction d’un point, puis la détermination d’un lieu géométrique se trouvaient ainsi remplacées par une représentation paramétrique, et une élimination. L’existence de méthodes canoniques d’élimination en théorie des polynômes est sans doute à l’origine de l’intérêt porté aux courbes algébriques, c’est-à-dire, grosso modo, à l’ensemble des points d’un plan où s’annule un polynôme.

Le rôle important de l’homogénéité dans la théorie des polynômes, aperçu au moment où s’élaborait la géométrie projective, a conduit à concevoir les modèles de courbes algébriques comme appartenant au plan projectif, qui a l’avantage d’être compact. D’autre part, si la conception initiale de la géométrie analytique était essentiellement une question de variables réelles, les géomètres algébristes ont été amenés à prendre comme corps de base le corps complexe à cause de la propriété fondamentale suivante: Tout polynôme de degré n à coefficients complexes a exactement n racines complexes, en tenant compte de leur ordre de multiplicité (propriété de clôture algébrique du corps C des nombres complexes); les courbes algébriques ont été les premiers exemples de variétés analytiques complexes.

Cela n’empêche pas, au moins dans le cas des polynômes à coefficients réels, pour aider l’imagination, de s’intéresser à la courbe réelle, lieu des points à coordonnées réelles, dans un plan affine ou même métrique déduit du plan projectif en spécialisant une droite à l’infini et en munissant le repère des propriétés adéquates (orthogonalité, normes): c’est la raison pour laquelle les mathématiques ont connu toute une abondante «flore» de courbes algébriques remarquables.

1. Courbes irréductibles

Considérons donc un plan projectif complexe, dans lequel les coordonnées homogènes sont x , y , z , et un polynôme (à coefficients réels ou complexes) homogène F de degré n ;

est l’équation d’une courbe algébrique. Le point A (a , b , c ) appartient à la courbe si:

Si l’on représente le même point par les coordonnéesa ,b ,c , où 0, on a:

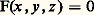
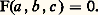
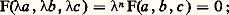on voit que ce fait est bien indépendant du choix des coordonnées homogènes et que des polynômes proportionnels définissent la même courbe.

Si F(x , y , z ) n’est pas décomposable sur le corps complexe en un produit de facteurs non constants, tout polynôme qui s’annule partout où s’annule F est de la forme:

par suite, si on appelle courbe irréductible l’ensemble des points où s’annule un polynôme indécomposable, la connaissance de la courbe entraîne celle de son équation (à un facteur constant non nul près).

La décomposition d’un polynôme quelconque en produit de facteurs irréductibles montre alors qu’une courbe algébrique générale doit être considérée comme constituée de composantes irréductibles , affectées chacune d’un exposant qui est un entier naturel, sa multiplicité . C’est ainsi que la courbe:

est formée de la droite double z = 0 et de la conique simple x ² + y ² 漣 z ² = 0.

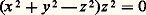Bien entendu, la notion de composante irréductible (et la multiplicité correspondante) sont des notions projectives, indépendantes du choix du repère, mais qui sont essentiellement liées au fait que le corps de base est algébriquement clos.

2. Tangentes

Intersection avec une droite

Considérons une droite projective joignant les point A(x ¹, y ¹, z ¹) et B(x ², y ², z ²) et son intersection avec la courbe F(x , y , z ) = 0. On obtient:

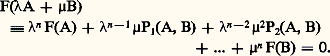Si tous les coefficients sont nuls, cette équation est une identité: tout point de la droite appartient à la courbe qui admet la droite comme composante irréductible.

Toute droite qui n’est pas composante de la courbe la coupe en n points (n étant le degré de F) compte tenu de leur ordre de multiplicité, et cet énoncé a exactement la même signification que l’affirmation: une équation algébrique de degré n admet n racines.

Supposons maintenant que A est un point de la courbe F(A) = 0, et faisons varier B arbitrairement; si le polynôme:

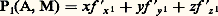n’est pas nul quel que soit M, toute droite passant par A coupe la courbe en ce point avec la multiplicité 1, à l’exception de la droite:

qui coupe la courbe en A avec une multiplicité au moins égale à 2. Le point A est alors appelé un point simple de la courbe, et la sécante exceptionnelle est appelée la tangente en A (en accord avec les formules différentielles de la géométrie analytique).

Lorsque: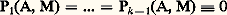

sont nuls quel que soit M, sans qu’il en soit ainsi de P^k , toute droite passant par A coupe la courbe en ce point avec la multiplicité k , à l’exception des droites qui vérifient P^k (A, M) = 0, qui coupent la courbe en A avec une multiplicité au moins égale à k + 1. Le point A est alors appelé un point multiple k-uple de la courbe, et les sécantes exceptionnelles sont appelées les tangentes en A.

Le point A est multiple k -uple de la courbe si toutes les dérivées d’ordre k 漣 1 de F sont nulles en ce point (et pas toutes les dérivées d’ordre k ). Bien entendu, un changement de variables projectif sur (, 猪) ou sur (x , y , z ) montre que les résultats précédents sont indépendants des repères.

Équation tangentielle

La question se pose alors de caractériser une courbe algébrique non plus comme l’ensemble de ses points, mais comme l’ensemble de ses tangentes. L’équation tangentielle est une condition nécessaire et suffisante entre les nombres u , v , w pour que la droite d’équation projective: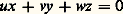

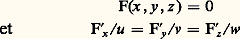soit tangente à la courbe. L’élimination de x , y , z entre les relations:

conduit à une équation tangentielle algébrique:

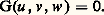Lorsque la courbe est irréductible (et n’est pas une droite), l’un des facteurs irréductibles de G représente l’enveloppe proprement dite, c’est-à-dire l’ensemble des tangentes; les autres facteurs irréductibles sont linéaires: chacun exprime le passage d’une droite par l’un des points singuliers de la courbe.

3. Quelques exemples

La courbe dont l’équation affine est:

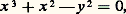c’est-à-dire dont l’équation projective, en coordonnées homogènes, est:

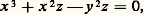est appelée cubique nodale (fig. 1).

Elle admet l’origine (x = 0, y = 0, z = 1) comme point double (de multiplicité 2); les deux tangentes en ce point sont les droites y = 梁 x . Le point (x = 0, y = 1, z = 0) est un point simple, pour lequel la tangente z = 0 coupe la courbe avec la multiplicité 3: on l’appelle un point d’inflexion . Les cubiques nodales sont toutes projectivement identiques. On rencontre le modèle métrique:

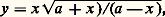qui a quelques propriétés liées à la géométrie du cercle et qu’on appelle la strophoïde . On rencontre également le modèle métrique:

appelé cubique de Tschirnhausen , pour lequel la longueur de l’arc est fonction rationnelle des coordonnées.

La courbe dont l’équation affine est:

est appelée cubique cuspidale (fig. 2). Elle admet l’origine (x = 0, y = 0, z = 1) comme point double (de multiplicité 2); il y a en ce point une tangente unique y = 0. Les cubiques cuspidales sont toutes projectivement identiques. On rencontre le modèle métrique: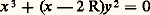

lié à la géométrie du cercle, et qu’on appelle la cissoïde . La développée de parabole est aussi une cubique nodale.

La courbe dont l’équation projective est:

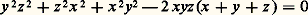est une quartique tricuspidale . Elle admet les trois sommets du repère (0, 0, 1; 0, 1, 0; 1, 0, 0) comme points doubles, en chacun desquels il y a une tangente unique: respectivement les droites x = y , z = x , y = z , concourantes au point unitaire. Lorsque le repère est choisi suivant un triangle équilatéral dont le point unitaire est le centre, la courbe métrique ainsi définie est connue sous le nom d’hypocycloïde à trois rebroussements (fig. 3).

4. Intersection de courbes algébriques

L’étude de l’intersection de deux courbes algébriques F et G de degrés respectifs m et n , qui n’ont aucune composante commune, a été faite par Bezout: il y a un nombre fini de points communs, et chacun est affecté d’un entier naturel, sa multiplicité (d’intersection); dénombrés avec cet élément de pondération, il y a mn points communs (sur le corps complexe). Ce théorème, tiré d’une étude attentive du résultant, n’a pas été apprécié à sa juste valeur par les non-spécialistes: faute d’avoir une définition explicite de la multiplicité d’intersection, ils voyaient dans le théorème de Bezout une espèce d’affirmation alchimique. On s’est borné à utiliser le théorème de Bezout dans certains cas simples: lorsque tous les points communs à F et G sont simples sur chacune d’elles, avec des tangentes distinctes, il y a exactement mn points communs. C’est ainsi que la courbe formée de m droites parallèles à Oy et la courbe formée de n droites parallèles à Ox se coupent aux mn sommets d’un quadrillage.

Un autre cas assez simple est celui où un point commun étant multiple d’ordre r pour F et d’ordre s pour G, il n’y a aucune droite commune aux deux faisceaux de tangentes en ce point: la multiplicité d’intersection est alors rs (et elle est supérieure dans le cas contraire).

La situation n’est devenue claire que lorsque G. Halphen eut montré comment, par une étude locale des courbes F et G en un point commun, on pouvait définir la multiplicité d’intersection.

Considérons par exemple les deux cubiques:

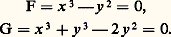Elles ont en commun trois points simples, avec la multiplicité 1, dont les coordonnées satisfont à: x ³ = 1, y = 1, et le point O qui est pour chacune d’elles un point double (r = s = 2) avec une seule tangente Ox . Ce point a la multiplicité d’intersection 6.

On le vérifie en portant x = t ², y = t ³, représentation paramétrique de F, dans G:

5. Étude locale d’un point singulier

Un point d’une courbe algébrique étant pris comme origine des coordonnées dans un modèle affine, l’étude du voisinage de O a été poursuivie par deux méthodes. Celle de Noether consiste à effectuer des transformations birationnelles ayant O pour point d’indétermination: elle relève des techniques de la géométrie algébrique. Celle de Enriques consiste à utiliser les développements de Puiseux: elle relève de l’analyse classique des fonctions d’une variable complexe.

La courbe (irréductible) F(x , y ) = 0, qui passe en O, définit y comme fonction algébrique de la variable complexe x , multiforme, dont certaines déterminations s’annulent pour x = 0.

On appelle branche algébroïde de la courbe F un ensemble de ces déterminations qui subit une permutation circulaire lorsque la variable complexe x décrit, dans le plan complexe, un petit cercle autour de l’origine. Si k est le nombre de déterminations constituant une branche, en faisant le changement de variable x = t ^k , chacune de ces déterminations devient une fonction entière de t : y = f (t ), et on passe de l’une à la suivante en changeant t en 﨣t , le coefficient 﨣 étant une racine primitive k -ième de l’unité.

Les propriétés arithmétiques des exposants qui figurent dans la série entière f (t ) ont été interprétées topologiquement (variété analytique complexe) et dans la géométrie infinitésimale de la courbe au voisinage de l’origine.

6. Courbes unicursales

Lorsqu’on a obtenu pour une courbe une représentation paramétrique uniforme, on détient un moyen commode pour l’étude de ses propriétés globales. C’est la raison de l’intérêt porté aux courbes unicursales, c’est-à-dire aux courbes qui, en coordonnées affines, admettent une représentation paramétrique rationnelle: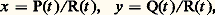

où P, Q, R sont des polynômes en t .

Les courbes unicursales sont souvent appelées les courbes rationnelles, car il résulte d’un théorème de Lüroth qu’elles sont les transformées birationnelles des droites projectives.

Les coniques (courbes algébriques irréductibles du second degré) sont rationnelles; elles admettent en effet la forme réduite projective:

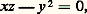qui conduit à la représentation:

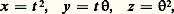où t , sont des paramètres complexes. De ce fait, on peut définir sur une conique le birapport de quatre points, les divisions homographiques et involutives. Ces notions peuvent être étendues à toute courbe rationnelle.

L’équation de la tangente au point courant d’une courbe paramétrique et la théorie des enveloppes montrent qu’il y a identité entre les courbes qui sont rationnelles du point de vue ponctuel et les courbes qui sont rationnelles du point de vue tangentiel.

Les cubiques rationnelles sont les cubiques à point double, dont nous avons donné les deux modèles; la cubique nodale citée ci-dessus admet pour représentation:

et la condition nécessaire et suffisante pour que trois points de la courbe soient alignés est t ¹t ²t ³ = 1.

La cubique cuspidale citée ci-dessus admet la représentation:

et la condition d’alignement de trois points est: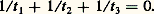

Les courbes rationnelles sont, parmi les courbes irréductibles de leur degré, celles qui ont les singularités les plus importantes, soit par leur nombre, soit par la complexité de leur structure: si une courbe rationnelle de degré n n’a que des points doubles de même nature que ceux des cubiques, ces points sont au nombre de:

C’est ainsi que la quartique tricuspidale citée plus haut est rationnelle; elle admet la représentation: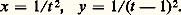

Mais la quartique d’équation (affine):

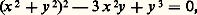que l’on appelle parfois trifolium (fig. 4), admet un seul point singulier, l’origine, qui est un point triple. En coupant cette courbe par les droites issues de O, on obtient sans difficulté la représentation paramétrique:

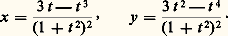L’existence de points doubles plus complexes (points infiniment voisins, contact des branches algébroïdes) permet de donner des exemples d’une nature différente.

La quartique (fig. 5) d’équation (affine):

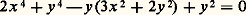admet deux points doubles; le point A (x = 0, y = 1), qui est un point nodal, et l’origine, qui est un point tacnodal (contact de deux branches algébroïdes). Cette quartique admet la représentation paramétrique:

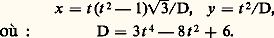La quartique (fig. 6) d’équation (affine):

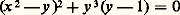admet un point double unique, à l’origine; c’est un point oscnodal (osculation de deux branches algébroïdes). Cette singularité suffit à assurer la rationalité, et la quartique proposée admet la représentation paramétrique:

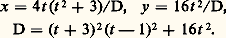7. Courbes elliptiques

Définitions

Nous avons dit que les cubiques sont rationnelles lorsqu’elles ont un point double. Les cubiques sans point singulier sont projectivement réductibles à la forme:

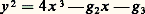(dans laquelle l’équation y = 0 doit avoir trois racines simples). Cette forme réduite, définie à une homothétie près, dépend du seul paramètre:

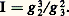La définition de la fonction elliptique face=F9828 p(u ) de Weierstrass met en évidence la représentation paramétrique x = face=F9828 p(u ), y = face=F9828 p (u ); c’est la raison pour laquelle les cubiques sans singularité sont appelées cubiques elliptiques.

L’argument:

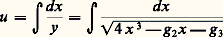est l’intégrale abélienne (de première espèce) attachée à la courbe. Plus généralement, deux fonctions elliptiques de mêmes périodes sont liées par une relation algébrique: elles constituent la représentation paramétrique d’une courbe algébrique dite courbe elliptique .

Si 諸 et 諸 sont deux périodes de base d’une fonction elliptique, on appelle parallélogramme de période tout parallélogramme admettant pour sommets les images des nombres complexes:

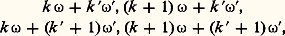où k , k sont des entiers relatifs. Dans un parallélogramme de période, une fonction elliptique prend le même nombre de fois toute valeur, et la somme des zéros est égale à la somme des pôles. Comme la fonction face=F9828 p(u ) a un pôle double à l’origine, la fonction:

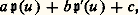fournit la condition nécessaire et suffisante d’alignement de trois points d’une cubique elliptique:

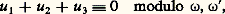諸 et 諸 étant deux périodes de base (cf. FONCTIONS ANALYTIQUES - Fonctions elliptiques et modulaire).

Si, dans l’étude des cubiques nodales, nous faisons le changement de représentation, u = log t la condition d’alignement devient:

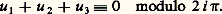Pour les cubiques cuspidales, u est le paramètre 1/t lui-même. On voit ainsi comment les cubiques rationnelles sont obtenues par dégénérescence des cubiques elliptiques.

Loi de groupe

Le théorème des points alignés (théorème de Lamé) consiste en ceci (fig. 7): coupons la cubique par trois droites A¹A²A³, B¹B²B³, C¹C²C³, telles que les points A¹B¹C¹ et A²B²C², respectivement, soient alignés. Alors A³B³C³ sont aussi alignés, car la somme totale des affixes est nulle.

Lorsque, dans la condition d’alignement, on fait u ¹ = u ² = u ³, on voit que la cubique elliptique a neuf points d’inflexion (la cubique nodale trois et la cubique cuspidale un seul):

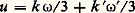(où k , k sont des entiers relatifs modulo 3). Ces points sont tels que toute droite qui en joint deux en contient un troisième, et cette propriété définit complètement la configuration. Un modèle métrique est obtenu en coupant un triangle équilatéral par la droite de l’infini et le cercle de rayon nul qui lui est concentrique.

Sur la figure 7, qui illustre le théorème des points alignés, nous avons placé B² en un point d’inflexion. Cela va nous permettre de montrer la structure de groupe abélien de la cubique elliptique, qui a B² pour élément neutre: deux points (tels que B¹ et B³) alignés sur B² sont opposés; quand trois points sont alignés chacun est opposé à la somme des deux autres. Ainsi, la somme A¹ + A³ est C² opposé de A². Cette opération est évidemment commutative et le théorème de Lamé établit son associativité:

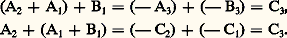La détermination du point (X, Y) somme des points (x ¹, y ¹) et (x ², y ²) se fait rationnellement et cette propriété est en liaison directe avec le théorème d’addition pour la fonction face=F9828 p(u ):

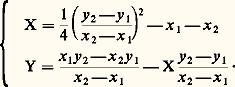D’un point arbitraire d’une cubique elliptique, on peut lui mener quatre tangentes, dont les contacts ont des arguments qui diffèrent d’une demi-période. D’après un théorème de Salmon, lorsque le point parcourt la cubique, le faisceau de ces quatre tangentes reste projectivement constant.

L’invariant (birapport symétrisé) de ce faisceau s’exprime au moyen de I, ou du quotient 諸 / 諸 des périodes: c’est la signification géométrique de la fonction modulaire:

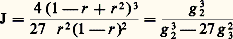Les méthodes utilisées pour l’étude des courbes elliptiques ont été généralisées aux courbes qui admettent une intégrale abélienne hyperelliptique; pour cette raison on les appelle courbes hyperelliptiques. L’extension aux courbes algébriques générales de la méthode paramétrique nécessite l’emploi des fonctions fuchsiennes introduites par Henri Poincaré.

8. Le genre

L’étude locale a permis de définir en chaque point d’une courbe algébrique une ou plusieurs branches algébroïdes: on appelle place la donnée d’un point et d’une branche algébroïde issue de ce point. L’ensemble des places d’une courbe est la riemannienne de cette courbe et on appelle cycle (parfois aussi diviseur ) de la courbe une combinaison linéaire formelle à coefficients entiers, positifs, négatifs ou nuls, des points de la riemannienne, un nombre fini seulement de points ayant un coefficient non nul. Les cycles d’une courbe forment un groupe abélien.

On appelle ordre d’un cycle la somme de ses coefficients. Un cycle est dit effectif (ou positif) si tous ses coefficients sont positifs ou nuls. Un cycle effectif ayant une signification géométrique simple peut, par exemple, être obtenu en envisageant, sur une courbe C irréductible coupée par une courbe algébrique 塚, chaque branche algébroïde affectée de la multiplicité de Bezout correspondante.

Plus généralement, étant donné une fraction rationnelle N(x , y , z )/D(x , y , z ), où N et D sont deux polynômes homogènes de même degré, dont aucun n’est nul sur toute la courbe C, on peut lui associer le cycle Z^N 漣 Z^D, différence des cycles associés au numérateur et au dénominateur: on vérifie en effet que toutes les fractions, formellement différentes, qui ont la même valeur le long de C, conduisent au même cycle. Les cycles associés aux fractions rationnelles sont d’ordre zéro et forment un sous-groupe abélien.

Deux cycles sont équivalents si leur différence est un cycle associé à une fraction rationnelle. On appelle série linéaire complète l’ensemble des cycles effectifs équivalents à un cycle effectif donné; cet ensemble a la structure d’un espace projectif: si n est l’ordre commun à tous ces cycles et r la dimension de l’espace projectif qu’ils constituent, on désigne la série linéaire par g ^{r n} . La classe d’équivalence d’un cycle est souvent appelée série linéaire virtuelle.

Deux séries linéaires étant données, prenons un cycle effectif (respectivement Z, Z ) dans chacune d’elles: le cycle Z + Z est effectif et définit une série linéaire complète, somme des deux séries linéaires données. Par exemple, les droites qui coupent une cubique elliptique en un point fixe découpent sur la courbe une g ¹². Deux g ¹² étant définies par les droites issues des points A et B de la courbe, la somme est la g ³⁴ découpée sur la courbe par les coniques qui passent par A et B ou par tout couple de points équivalents.

Le théorème du reste de Brill-Noether énonce que tous les cycles effectifs (s’il en existe) obtenus par différence des cycles de deux séries linéaires forment une série linéaire. Il a trouvé de nombreuses applications à l’étude des intersections complètes. C’est ainsi, par exemple, que si, parmi les neuf points communs à deux cubiques, il y en a six qui sont situés sur une même conique, les trois autres sont alignés.

Introduit par Riemann, le genre p d’une courbe algébrique irréductible est le nombre des intégrales abéliennes de première espèce, attachées à la courbe, linéairement indépendantes. Les différentielles holomorphes sur la courbe définissent des cycles équivalents qui constituent la classe canonique K: les cycles canoniques effectifs constituent la série canonique qui a l’ordre 2 p 漣 2 et la dimension p 漣 1. Sur une courbe rationnelle, K a l’ordre 漣 2. Sur une courbe elliptique, K a l’ordre zéro; seul le cycle nul appartient à la série canonique qui a la dimension zéro. Cela tient à ce que, selon un théorème de Liouville, les seules fonctions elliptiques holomorphes sont les constantes.

Soit G un cycle d’une série linéaire g ^{r n} : si la classe K 漣 G contient des cycles effectifs, on dit que la série est spéciale, et le nombre de cycles effectifs de K 漣 G linéairement indépendants est appelé son indice de spécialité i . Lorsqu’il n’y en a pas (ce qui est, par exemple, le cas pour n 礪 2p 漣 2), la série g ^{r n} est dite régulière.

La signification géométrique du genre est alors donnée par les deux théorèmes suivants: Si une série linéaire complète g ^{r n} est régulière, on a r = n 漣 p (Riemann). Plus généralement, si une série linéaire complète g ^{r n} a l’indice de spécialité i , on a r = n 漣 p + i (Riemann-Roch).

L’ensemble des séries linéaires complètes g ^{i p} d’ordre p peut, par application du théorème du reste, être muni d’une structure de variété abélienne de dimension p : c’est la jacobienne de la courbe.

La classe canonique et, par conséquent, le genre p ont été introduits d’une façon purement algébrique par Enriques, au moyen d’une construction tirée du jacobien. Liée à la théorie des enveloppes, cette construction élégante perd malheureusement sa valeur en géométrie algébrique abstraite sur les corps de caractéristique non nulle.

Une autre définition du genre a été présentée par Weierstrass, qui s’intéresse aux cycles associés aux pôles d’une fraction rationnelle définie sur une courbe irréductible. Une place P munie de la multiplicité n peut être l’unique pôle d’une fraction rationnelle, à condition que n ne fasse pas partie d’un certain ensemble de p entiers, les «lacunes», inférieures à 2 p 漣 1. Si P pris sur la riemannienne est pris hors d’un certain ensemble fini, les lacunes sont 1, 2, ..., p . En géométrie algébrique abstraite, sur un corps de caractéristique non nulle, la seconde partie du théorème de Weierstrass n’est pas vraie: il peut arriver que pour toute place P les lacunes diffèrent de 1, 2, ..., p .

Encyclopédie Universelle. 2012.